Для начала ответим себе на вопрос, что такое электрический ток. Простая батарейка, стоящая на столе, сама по себе ток не создает. И фонарик, лежащий на столе, ток через свои светодиоды просто так, ни с того ни с сего, не создаст. Чтобы появился ток, что-то куда-то должно потечь, хотя бы начать двигаться, а для этого цепь из светодиодов фонарика и батарейки необходимо замкнуть. Не даром, в былые времена электрический ток сравнивали с движением некой заряженной жидкости.
На самом деле мы теперь знаем, что электрический ток — это направленное движение заряженных частиц, и что более близким к реальности аналогом был бы заряженный газ, — газ заряженных частиц, движущийся под действием электрического поля. Но обо всем по порядку.
Электрический ток — это направленное движение заряженных частиц
Итак, электрический ток — это движение заряженных частиц, но даже хаотичное движение заряженных частиц — это тоже движение, однако оно еще не является током. Так и молекулы жидкости, все время пребывающие в тепловом движении, течения не создают, ведь суммарное перемещение всего объема покоящейся жидкости ровно нулю.
Чтобы возникло течение жидкости, должно возникнуть суммарное перемещение, то есть общее движение молекул жидкости должно стать направленным. Так хаотичное движение молекул сложится с направленным движением всего объема, и возникнет течение всего объема жидкости.
Аналогично обстоит дело и с электрическим током — направленное движение электрически заряженных частиц — есть электрический ток. Скорость теплового движения заряженных частиц, например в металле, измеряется сотнями метров в секунду, однако при направленном движении, когда в проводнике установлен какой-то определенный ток, скорость общего движения частиц измеряется долями и единицами миллиметров в секунду.
Так, если в металлическом проводнике сечением 1 кв. мм течет постоянный ток равный 10 А, то средняя скорость упорядоченного движения электронов составит от 0,6 до 6 миллиметров в секунду. Это уже будет электрическим током. И этого медленного движения электронов достаточно, чтобы проводник, например из нихрома, неплохо разогрелся, повинуясь закону Джоуля-Ленца.
Скорость частиц — это не скорость распространения электрического поля!
Отметим, что ток начинается в проводнике почти мгновенно по всему объему, то есть распространяется это «движение» по проводнику со скоростью света, а вот движение непосредственно самих заряженных частиц в 100 миллиардов раз медленнее. Можно рассмотреть аналогию с трубой, по которой течет жидкость.
Для существования электрического тока необходимы заряженные частицы
Электроны в металлах и в вакууме, ионы в растворах электролитов — служат носителями заряда и обеспечивают наличие тока в разных веществах. В металлах электроны очень подвижны, некоторые из них свободно могут двигаться от атома к атому, словно газ заполняя пространство между узлами кристаллической решетки.
В электронных лампах электроны покидают катод в процессе термоэлектронной эмиссии, устремляясь под действием электрического поля к аноду. В электролитах молекулы распадаются в воде на положительно и отрицательно заряженные части, и становятся ионами — свободными носителями заряда в электролитах. То есть везде, где может существовать электрический ток, есть свободные носители заряда, способные перемещаться под действием электрического поля. Это и есть первое условие существования электрического тока — наличие свободных носителей заряда.
Второе условие существования электрического тока — на заряд должны действовать сторонние силы
Если теперь взглянуть на проводник, допустим это медный провод, то можно задаться вопросом: а что нужно для того, чтобы электрический ток в нем возник? Заряженные частицы, электроны, есть, они способны свободно перемещаться.
Что заставит их двигаться? Известно, что электрически заряженная частица взаимодействует с электрическим полем. Следовательно в проводнике необходимо создать электрическое поле, тогда в каждой точке проводника возникнет потенциал, между концами проводника будет иметь место разность потенциалов, и электроны придут в движение по направлению поля — по направлению от «-» к «+», то есть в направлении против вектора напряженности электрического поля. Электрическое поле станет ускорять электроны, увеличивая их (кинетическую и магнитную) энергию.
В итоге, если мы рассматриваем просто приложенное снаружи к проводнику электрическое поле (поместили проводник в электрическое поле вдоль силовых линий), то электроны станут скапливаться у одного конца провода, и на этом конце возникнет отрицательный заряд, а поскольку с другого конца провода электроны сместились, то на нем будет иметь место заряд положительный.
В результате электрическое поле проводника, заряженного приложенным снаружи электрическим полем, будет такого направления, чтобы своим действием ослаблять внешнее электрическое поле.
Процесс перераспределения зарядов протечет почти мгновенно, и по его завершении ток в проводнике прекратится. Результирующее электрическое поле внутри проводника станет равным нулю, а напряженность по краям окажется равной по модулю, но противоположной по направлению к приложенному снаружи электрическому полю.
Если электрическое поле в проводнике создается источником постоянного тока, например батарейкой, то такой источник станет для проводника источником сторонних сил, то есть тем источником, который создаст в проводнике постоянную ЭДС, и будет поддерживать разность потенциалов. Очевидно, чтобы ток источником сторонних сил поддерживался, цепь должна быть замкнутой.
На чтение 26 мин. Просмотров 537
Что такое электрический ток
Электрический ток — направленное движение электрически заряженных частиц под воздействием электрического поля. Такими частицами могут являться: в проводниках – электроны, в электролитах – ионы (катионы и анионы), в полупроводниках – электроны и, так называемые, «дырки» («электронно-дырочная проводимость»). Также существует «ток смещения», протекание которого обусловлено процессом заряда емкости, т. изменением разности потенциалов между обкладками. Между обкладками никакого движения частиц не происходит, но ток через конденсатор протекает.
В теории электрических цепей за ток принято считать направленное движение носителей заряда в проводящей среде под действием электрического поля.
Током проводимости (просто током) в теории электрических цепей называют количество электричества, протекающего за единицу времени через поперечное сечение проводника: i=q/t, где i — ток. А; q = 1,6·109 — заряд электрона, Кл; t — время, с.
Это выражение справедливо для цепей постоянного тока. Для цепей переменного тока применяют так называемое мгновенное значение тока, равное скорости изменения заряда во времени: i(t)= dq/dt.
Первым условием длительного существования электрического тока рассматриваемого вида является наличие источника, или генератора, поддерживающего разность потенциалов между носителями зарядов. Второе условие — замкнутость пути. В частности, для существования постоянного тока необходимо наличие замкнутого пути, по которому заряды могут перемещаться внутри контура без изменения их значения.
Как известно, в соответствии с законом сохранения электрических зарядов они не могут создаваться или исчезать. Поэтому, если любой объем пространства, где протекают электрические токи, окружить замкнутой поверхностью, то ток, втекающий в этот объем, должен быть равен току, вытекающему из него.
Подробнее об этом: Условия существования электрического тока
Замкнутый путь, по которому течет электрический ток, называют цепью электрического тока, или электрической цепью. Электрическая цепь — делится на две части: внутреннюю, в которой электрически заряженные частицы движутся против направления электростатических сил, и внешнюю часть, в которой эти частицы движутся в направлении электростатических сил. Концы электродов, к которым подсоединяется внешняя цепь, называются зажимами.
Итак, электрический ток возникает тогда, когда на участке электрической цепи появляется электрическое поле, или разность потенциалов между двумя точками проводника. Разность потенциалов между двумя точками электрической цепи называют напряжением или падением напряжения на этом участке цепи.
Вместо термина «ток» («величина тока») часто применяется термин «сила тока». Однако последний нельзя назвать удачным, так как сила тока не есть какая-либо сила в буквальном смысле этого слова, а только интенсивность движения электрических зарядов в проводнике, количество электричества, проходящего за единицу времени через площадь поперечного сечения проводника. Ток характеризуется силой тока, которая в системе СИ измеряется в амперах (А), и плотностью тока, которая в системе СИ измеряется в амперах на квадратный метр.
1А = 1Кл / с.
В общем случае, обозначив ток буквой i, а заряд q, получим:
i = dq / dt.
Единица тока называется ампер (А).
Ток в проводнике равен 1 А, если через поперечное сечение проводника за 1 сек проходит электрический заряд, равный 1 кулон.
Рис. Направленное движение электронов в проводнике
Если вдоль проводника действует напряжение, то внутри проводника возникает электрическое поле. При напряженности поля Е на электроны с зарядом е действует сила f = Ее. Величины f и Е векторные. В течение времени свободного пробега электроны приобретают направленное движение наряду с хаотическим. Каждый электрон имеет отрицательный заряд и получает составляющую скорости, направленную противоположно вектору Е (рис. Упорядоченное движение, характеризуемое некоторой средней скоростью электронов vcp, определяет протекание электрического тока.
Электроны могут иметь направленное движение и в разреженных газах. В электролитах и ионизированных газах протекание тока в основном обусловлено движением ионов. В соответствии с тем, что в электролитах положительно заряженные ионы движутся от положительного полюса к отрицательному, исторически направление тока было принято обратным направлению движения электронов.
За направление тока принимается направление, в котором перемещаются положительно заряженные частицы, т. направление, противоположное перемещению электронов. В теории электрических цепей за направление тока в пассивной цепи (вне источников энергии) взято направление движения положительно заряженных частиц от более высокого потенциала к более низкому. Такое направление было принято в самом начале развития электротехники и противоречит истинному направлению движения носителей заряда — электронов, движущихся в проводящих средах от минуса к плюсу.
Направление электрического тока в электролите и свободных электронов в проводнике
Величина, равная отношению тока к площади поперечного сечения S, называются плотностью тока: I / S
При этом предполагается, что ток равномерно распределен по сечению проводника. Плотность тока в проводах обычно измеряется в А/мм2.
По типу носителей электрических зарядов и среды их перемещения различают токи проводимости и токи смещения. Проводимость делят на электронную и ионную. Для установившихся режимов различают два вида токов: постоянный и переменный.
Электрическим током переноса называют явление переноса электрических зарядов заряженными частицами или телами, движущимися в свободном пространстве. Основным видом электрического тока переноса является движение в пустоте элементарных частиц, обладающих зарядом (движение свободных электронов в электронных лампах), движение свободных ионов в газоразрядных приборах.
Электрическим током смещения (током поляризации) называют упорядоченное движение связанных носителей электрических зарядов. Этот вид тока можно наблюдать в диэлектриках.
Полный электрический ток — скалярная величина, равная сумме электрического тока проводимости, электрического тока переноса и электрического тока смещения сквозь рассматриваемую поверхность.
Постоянным называют ток, который может изменяться по величине, но не изменяет своего знака сколь угодно долгое время. Подробнее об этом читайте здесь: Постоянный ток
Ток намагниченности — постоянный микроскопический (амперовый) ток, являющийся причиной существования собственного магнитного поля намагниченных веществ.
Переменным называют ток, который периодически изменяется как по величине, так и по знаку. Величиной, характеризующей переменный ток, является частота (в системе СИ измеряется в герцах), в том случае, когда его сила изменяется периодически.
Переменный ток высокой частоты вытесняется на поверхность проводника. Токи высокой частоты применяется в машиностроении для термообработки поверхностей деталей и сварки, в металлургии для плавки металлов. Переменные токи подразделяют на синусоидальные и несинусоидальные. Синусоидальным называют ток, изменяющийся по гармоническому закону:
i = Im sin wt,
где Im, — амплитудное (наибольшее) значение тока, А,
Скорость изменения переменного тока характеризуется его частотой, определяемой как число полных повторяющихся колебаний в единицу времени. Частота обозначается буквой f и измеряется в герцах (Гц). Так, частота тока в сети 50 Гц соответствует 50 полным колебаниям в секунду. Угловая частота w — скорость изменения тока в радианах в секунду и связана с частотой простым соотношением:
w = 2пиf
Установившиеся (фиксированные) значения постоянного и переменного токов обозначают прописной буквой I неустановившиеся (мгновенные) значения — буквой i. Условно положительным направлением тока считают направление движения положительных зарядов.
Переменный ток — это ток, который изменяется по закону синуса с течением времени.
Под переменным током также подразумевают ток в обычных одно- и трёхфазных сетях. В этом случае параметры переменного тока изменяются по гармоническому закону.
Поскольку переменный ток изменяется во времени, простые способы решения задач, пригодные для цепей постоянного тока, здесь непосредственно неприменимы. При очень высоких частотах заряды могут совершать колебательное движение — перетекать из одних мест цепи в другие и обратно. При этом, в отличие от цепей постоянного тока, токи в последовательно соединённых проводниках могут оказаться неодинаковыми.
Ёмкости, присутствующие в цепях переменного тока, усиливают этот эффект. Кроме того, при изменении тока сказываются эффекты самоиндукции, которые становятся существенными даже при низких частотах, если используются катушки с большой индуктивностью.
При сравнительно низких частотах цепи переменного тока можно по-прежнему рассчитывать с помощью правил Кирхгофа, которые, однако, необходимо соответствующим образом модифицировать.
Цепь, в которую входят разные резисторы, катушки индуктивности и конденсаторы, можно рассматривать, как если бы она состояла из обобщённых резистора, конденсатора и катушки индуктивности, соединённых последовательно.
Рассмотрим свойства такой цепи, подключённой к генератору синусоидального переменного тока. Чтобы сформулировать правила, позволяющие рассчитывать цепи переменного тока, нужно найти соотношение между падением напряжения и током для каждого из компонентов такой цепи.
Конденсатор играет совершенно разные роли в цепях переменного и постоянного токов. Если, например, к цепи подключить электрохимический элемент, то конденсатор начнёт заряжаться, пока напряжение на нём не станет равным ЭДС элемента. Затем зарядка прекратится и ток упадёт до нуля.
Если же цепь подключена к генератору переменного тока, то в один полупериод электроны будут вытекать из левой обкладки конденсатора и накапливаться на правой, а в другой — наоборот.
Эти перемещающиеся электроны и представляют собой переменный ток, сила которого одинакова по обе стороны конденсатора. Пока частота переменного тока не очень велика, ток через резистор и катушку индуктивности также одинаков.
В устройствах-потребителях переменного тока переменный ток часто выпрямляется выпрямителями для получения постоянного тока.
Проводники электрического тока
Электрический ток во всех его проявлениях представляет собой кинетическое явление, аналогичное течению жидкости в замкнутых гидравлических системах. По аналогии процесс движения тока называется «течением» (ток течет).
Материал, в котором течёт ток, называется проводником. Некоторые материалы при низких температурах переходят в состояние сверхпроводимости. В таком состоянии они не оказывают почти никакого сопротивления току, их сопротивление стремится к нулю.
Во всех остальных случаях проводник оказывает сопротивление течению тока и в результате часть энергии электрических частиц превращается в тепло. Силу тока можно рассчитать по закону Ома для участка цепи и закону Ома для полной цепи.
Скорость движения частиц в проводниках зависит от материала проводника, массы и заряда частицы, окружающей температуры, приложенной разности потенциалов и составляет величину, намного меньшую скорости света. Несмотря на это, скорость распространения собственно электрического тока равна скорости света в данной среде, то есть скорости распространения фронта электромагнитной волны.
Как ток влияет на организм человека
Ток, пропущенный через организм человека или животного, может вызвать электрические ожоги, фибрилляцию или смерть. С другой стороны, электрический ток используют в реанимации, для лечения психических заболеваний, особенно депрессии, электростимуляцию определённых областей головного мозга применяют для лечения таких заболеваний, как болезнь Паркинсона и эпилепсия, водитель ритма, стимулирующий сердечную мышцу импульсным током, используют при брадикардии. В организме человека и животных ток используется для передачи нервных импульсов.
По технике безопасности, минимально ощутимый человеком ток составляет 1 мА. Опасным для жизни человека ток становится начиная с силы примерно 0,01 А. Смертельным для человека ток становится начиная с силы примерно 0,1 А. Безопасным считается напряжение менее 42 В.
Электрический ток — это направленное (упорядоченное, то есть не хаотичное) движение электрически заряженных частиц или заряженных макроскопических тел. Под заряженными частицами, обычно, подразумеваются электроны или ионы, а под макроскопическими (macroscopic — видимые невооруженным глазом) — крупные частицы, например, заряженные капли дождя. Ток возникает при наличии электрического поля. Разберемся с тем как определяется направление электрического тока.
Электрический ток в разных веществах
Электрический ток возникает в самых разных веществах, которые могут находиться в различных агрегатных состояниях. Рассмотрим некоторые примеры, демонстрирующие возникновение направленного потока заряженных частиц в твердых, жидких и газообразных средах:
- В металлах имеется много свободных электронов, которые являются главным источником тока;
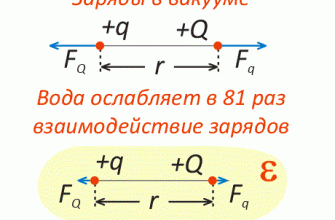
- Электролиты — это жидкости, проводящие электрический ток. Водные растворы кислот, щелочей, солей — все это примеры электролитов. Попадая в воду молекулы этих веществ распадаются на ионы, представляющие собой заряженные атомы или группы атомов, имеющие положительный (катионы) или отрицательный (анионы) электрические заряды. Катионы и анионы образуют электрический ток в электролитах;
- В газах и плазме ток создается за счет движения электронов и положительно заряженных ионов;
- В вакууме — за счет электронов, вылетающих с поверхности металлических электродов.
В каком направлении течет ток
За направление тока принято направление движения положительно заряженных частиц; если же ток создается отрицательно заряженными частицами (например, электронами), то направление тока считается противоположным направлению движения частиц.
Возникает вопрос: почему не был принят очевидный вариант направления, совпадающий с направлением движения электронов? Для того, чтобы это стало понятно, надо немного окунуться в историю физики.
Почему надо знать историю физических открытий
Природу электрических явлений пытались объяснить многие исследователи задолго до открытия электрона (1897 г. Впервые к пониманию о существовании двух типов зарядов — положительных и отрицательных пришел американский физик Бенджамин Франклин в 1747 г. На основе своих наблюдений он предположил (выдвинул гипотезу), что существует некая “электрическая материя”, состоящая из мелких, невидимых частиц. Он же первым ввел обозначение для электрических зарядов “−” и “+”. Франклин предложил считать, что если тело наполняется электрической материей, то оно заряжается положительно, а если оно теряет электричество, то заряжается отрицательно. В случае замыкания (соединения) цепи положительный заряд потечет туда, где его нет, то есть к “минусу”. Эта плодотворная гипотеза стала популярной, получила свое признание среди ученых, вошла в справочники и учебные пособия.
Конечно, после открытия отрицательно заряженного электрона, эта “нестыковка” реального направления движения с ранее общепринятым была обнаружена. Однако, мировым научным сообществом было принято решение оставить в силе предыдущую формулировку о направлении тока, поскольку в большинстве практических случаев это ни на что не влияет.
В случае необходимости, для объяснения отдельных физических эффектов в полупроводниках и искусственных материалах (гетероструктурах), принимается во внимание настоящее направление движения электронов.
Тест по теме
Закон Ома для участка цепи, безусловно, можно описать известной из школьного курса физики формулой: I=U/R, но некоторые изменения и уточнения внести, думаю, стоит. Возьмем замкнутую электрическую цепь и рассмотрим ее участок между точками 1-2. Для простоты я взял участок электрической цепи, не содержащий источников ЭДС (Е).
Итак, закон Ома для рассматриваемого участка цепи имеет вид:
- I – ток, протекающий по участку цепи.
- R – сопротивление этого участка.
- φ1-φ2 – разность потенциалов между точками 1-2.
Если учесть, что разность потенциалов это напряжение, то приходим к производной формулы закона Ома, которая приведена в начале страницы: U=I*R. Это формула закона Ома для пассивного участка цепи (не содержащего источников электроэнергии).
Интересно по теме: Как проверить стабилитрон.
В неразветвленной электрической цепи (рис. 2) сила тока во всех участках одинакова, а напряжение на любом участке определяется его сопротивлением:
- U1=I*R1
- U2=I*R2
- Un=I*Rn
- U=I*(R1+R2+…+Rn
Отсюда можно получить формулы, которые пригодятся при практических вычислениях. Например:
Расчет сложных (разветвленных) цепей осуществляется с помощью законов Кирхгофа.
Закон Ома для участка цепи.
Для ЭДС
Перед тем как рассмотреть закон Ома для полной (замкнутой) цепи приведу правило знаков для ЭДС, которое гласит:
Если внутри источника ЭДС ток идет от катода (-) к аноду (+) (направление напряженности поля сторонних сил совпадает с направлением тока в цепи, то ЭДС такого источника считается положительной. В противном случае – ЭДС считается отрицательной.
Практическим применением этого правила является возможность приведения нескольких источников ЭДС в цепи к одному с величиной E=E1+E2+…+En, естественно, с учетом знаков, определяемых по вышеприведенному правилу. Например (рис. 3) E=E1+E2-E3. При отсутствии встречно включенного источника E3 (на практике так почти никогда не бывает) имеем широко распространенное последовательное включение элементов питания, при котором их напряжения суммируются.
Для полной цепи
Закон Ома для полной цепи – его еще можно назвать закон ома для замкнутой цепи, имеет вид I=E/(R+r). Приведенная формула закона Ома содержит обозначение r, которое еще не упоминалось. Это внутреннее сопротивление источника ЭДС. Оно достаточно мало, в большинстве случаев при практических расчетах им можно пренебречь (при условии, что R>>r – сопротивление цепи много больше внутреннего сопротивления источника). Однако, когда они соизмеримы, пренебрегать величиной r нельзя.
Как вариант можно рассмотреть случай, при котором R=0 (короткое замыкание). Тогда приведенная формула закона Ома для полной цепи примет вид: I=E/r, то есть величина внутреннего сопротивления будет определять ток короткого замыкания. Такая ситуация вполне может быть реальной. Закон Ома рассмотрен здесь достаточно бегло, но приведенных формул достаточно для проведения большинства расчетов, примеры которых, по мере размещения других материалов я буду приводить.
Полноценную цепь составляет уже участок (участки), а также источник ЭДС. То есть, фактически к существующему резистивному компоненту участка цепи добавляется внутреннее сопротивление источника ЭДС. Поэтому логичным является некоторое изменение выше рассмотренной формулы:
I = U / (R + r)
Конечно, значение внутреннего сопротивления ЭДС в законе Ома для полной электрической цепи можно считать ничтожно малым, правда во многом это значение сопротивления зависит от структуры источника ЭДС. Тем не менее, при расчетах сложных электронных схем, электрических цепей с множеством проводников, наличие дополнительного сопротивления является важным фактором.
Как для участка цепи, так и для полной схемы следует учитывать естественный момент – использование тока постоянной или переменной величины. Если отмеченные выше моменты, характерные для закона Ома, рассматривались с точки зрения использования постоянного тока, соответственно с переменным током всё выглядит несколько иначе.
Для переменного тока
Переменный ток отличается от постоянного тем, что он изменяется с определенными временными периодами. Конкретно он изменяет свое значение и направление. Чтобы применить закон Ома здесь нужно учитывать, что сопротивление в цепи с постоянным током может отличатся от сопротивления в цепи с током переменным. И отличается оно в том случае если в цепи применены компоненты с реактивным сопротивлением. Реактивное сопротивление может быть индуктивным (катушки, трансформаторы, дроссели) и емкостными (конденсатор).
Если мы схематически представим, как с течением времени меняются эти два значения, у нас получится синусоида. И напряжение, и сила тока от нуля поднимаются до максимального значения, затем, опускаясь, проходят через нулевое значение и достигают максимального отрицательного значения. После этого снова поднимаются через нуль до максимального значения и так далее. Когда говорится, что сила тока или напряжение имеет отрицательное значение, здесь имеется ввиду, что они движутся в обратном направлении.
Весь процесс происходит с определенной периодичностью. Та точка, где значение напряжения или силы тока из минимального значения поднимаясь к максимальному значению проходит через нуль называется фазой.
Для замкнутой цепи
На самом деле, это только предисловие. Вернемся к реактивному и активному сопротивлению. Отличие активного сопротивления от реактивного в том, что в цепи с активным сопротивлением фаза тока совпадает с фазой напряжения. То есть, и значение силы тока, и значение напряжения достигают максимума в одном направлении одновременно. В таком случае наша формула для расчета напряжения, сопротивления или силы тока не меняется.
Следствия закона Ома.
Если же цепь содержит реактивное сопротивление, фазы тока и напряжения сдвигаются друг от друга на ¼ периода. Это означает, что, когда сила тока достигнет максимального значения, напряжение будет равняться нулю и наоборот. Когда применяется индуктивное сопротивление, фаза напряжения «обгоняет» фазу тока. Когда применяется емкостное сопротивление, фаза тока «обгоняет» фазу напряжения.
Формула для расчета падения напряжения на индуктивном сопротивлении:
U = I ⋅ ωL
Где L – индуктивность реактивного сопротивления, а ω – угловая частота (производная по времени от фазы колебания).
Формула для расчета падения напряжения на емкостном сопротивлении:
U = I / ω ⋅ С
С – емкость реактивного сопротивления.
Эти две формулы – частные случаи закона Ома для переменных цепей.
Полный же будет выглядеть следующем образом:
I = U / Z
Здесь Z – полное сопротивление переменной цепи известное как импеданс.
Сфера применения
Закон Ома не является базовым законом в физике, это лишь удобная зависимость одних значений от других, которая подходит почти в любых ситуациях на практике. Поэтому проще будет перечислить ситуации, когда закон может не срабатывать:
- Если есть инерция носителей заряда, например, в некоторых высокочастотных электрических полях;
- В сверхпроводниках;
- Если провод нагревается до такой степени, что вольтамперная характеристика перестает быть линейной. Например, в лампах накаливания;
- В вакуумных и газовых радиолампах;
- В диодах и транзисторах.
Закон Ома для замкнутой цепи
Подобная интерпретация подразумевает наличие источника питания, а также проводника, по которому протекает ток. В этом случае, помимо сопротивления на отдельно взятом участке следует учитывать и то, которое возникает в ИП. Учитывая эти факторы, можно сказать, что сила тока будет равна отношению электродвижущей силы к сумме сопротивлений.
где Е – ЭДС, Rвн – внешнее сопротивление, а r соответственно внутреннее.
Закон Ома для замкнутой цепи можно объяснить доступным языком. Электродвижущая сила по определению должна полноценно обеспечивать постоянную разницу потенциалов, и эта сила может иметь неприродное происхождение: химическое, если в качестве источника используется батарейка или механическая, в случае подключения к электрической цепи генератора. При подключении медной проволоки с идентичным сечением к батарейке и аккумулятору. Эффект должен быть таким, что по этому проводнику, в котором сопротивление практически отсутствует, должен пойти ток с величиной, стремящейся к бесконечности. Однако этого не происходит и разница в показателях будет существенной, а во втором случае, проволока и вовсе может перегореть. Именно поэтому в расчет берется внутреннее сопротивление источника питания, чтобы описать подобное явление.
Закон Ома для неоднородного участка цепи
Перед тем, как записать формулу для подобной интерпретации закона, следует разобраться в таких понятиях, как линейные и нелинейные участки цепи.
Если сопротивление никаким образом не зависит от тока и подаваемого напряжения, то с ростом второго параметра, первый будет прямо пропорционально возрастать и наоборот, то есть зависимость можно описать прямой линией. Подобная зависимость относится к линейным участкам цепи и сопротивление имеет аналогичное название.
Однако вышеизложенный вариант считается идеальным и его можно смоделировать лишь в идеальных условиях, что фактически невозможно, ведь, как минимум, окружающая среда вносит свои коррективы. В этом случае, рост напряжения не будет прямо пропорциональным силе тока и на графике зависимость будет изображаться в виде кривой.
На рисунке изображено два графика, первый из которых описывает линейную зависимость, а второй нелинейную.
Чтобы отчетливо понимать разницу между этими понятиями, рассмотрим принцип работы обычной электрической лампы накаливания. При прохождении тока по нити, температура в значительной степени повышается, что приводит к заметному росту сопротивления. Соответственно, при возрастании напряжения, сила тока будет увеличиваться медленнее, то есть не линейно.
Примечание: в некоторых ситуациях, некоторыми внешними факторами пренебрегают по причине того, что они очень незначительны и в числовом эквиваленте никоим образом не могут повлиять на общую картину. Это значит, что нелинейная зависимость на графике фактически совпадает с линейной.
Учитывая вышесказанное, можно установить следующую зависимость:
I = U/ R = (f1 – f2) + E/ R,
Где f1 и f2 – потенциалы (соответственно f1 – f2 называется разницей потенциалов), E – ЭДС неоднородного участка цепи, а R – суммарное сопротивление на этом же участке.
Нужно упомянуть и о том, что электродвижущая сила не всегда в этом случае будет иметь положительное значение. Если направление тока источника будет аналогичным с направлением в электрической сети, протонов будет больше, чем электронов (положительных и отрицательных частиц), то в этом случае величина E будет иметь значение со знаком «+», в иной ситуации, этот параметр будет со знаком «-».
Закон Ома для переменного тока
Если в электроцепи имеется емкость или инертность, то этот факт следует однозначно учитывать при расчётах силы тока. Они имеют собственные показатели сопротивления, что приводит к ситуации, которая будет иметь переменный характер. В случае Закона Ома для переменного тока формула записывается следующим образом:
I – сила тока, U – напряжение, а Z – суммарное значение сопротивления на всех участках электрической цепи (этот параметр именуется еще, как импеданс).
Как говорилось изначально, закон Ома считается эмпирическим. Это обозначает то, что он может не всегда работать и выполнять вычисления на его основе не представляется возможным. Подобная ситуация может сложиться в нескольких случаях:
- в ситуации, когда электросеть имеет высокую частоту и электромагнитное поле может сильно изменяться за короткие промежутки времени;
- при наличии проводников, которые обладают свойствами сверхпроводимости, расположенных в условиях низких температурных показателей;
- при перегреве проводника под воздействием проходящего по нему тока, отношение напряжения и сопротивления может носить переменный, неоднородный характер;
- если проводник (диэлектрик) находится под высоким напряжением;
- светодиодных лампах;
- в полупроводниках и аналогичных устройствах.
На основе этого закона, можно произвести вывод некоторых формул математическим путем. С их помощью можно производить разнообразные расчеты.
Метода треугольника закона Ома
Закон Ома – очень простой и полезный инструмент для анализа электрических цепей. Он так часто используется при изучении электричества и электроники, что студент должен запомнить его. Если вы не очень хорошо умеете работать с формулами, то для его запоминания существует простой прием, помогающий использовать его для любой величины, зная две других. Сначала расположите буквы E, I и R в виде треугольника следующим образом:
Рисунок 5 – Треугольник закона Ома
Если вы знаете E и I и хотите определить R, просто удалите R с картинки и посмотрите, что осталось:
Рисунок 6 – Закон Ома для определения R
Если вы знаете E и R и хотите определить I, удалите I и посмотрите, что осталось:
Рисунок 7 – Закон Ома для определения I
Наконец, если вы знаете I и R и хотите определить E, удалите E и посмотрите, что осталось:
Рисунок 8 – Закон Ома для определения E
В конце концов, вам придется научиться работать с формуми, чтобы серьезно изучать электричество и электронику, но этот совет может облегчить запоминание ваших первых вычислений. Если вам удобно работать с формулами, всё, что вам нужно сделать, это зафиксировать в памяти E = IR и вывести из нее две другие формулы, когда они вам понадобятся!
Значение Закона Ома
Закон Ома определяет силу тока в электрической цепи при заданном напряжении и известном сопротивлении. Он позволяет рассчитать тепловые, химические и магнитные действия тока, так как они зависят от силы тока.
Закон Ома является чрезвычайно полезным в технике(электронной/электрической), поскольку он касается трех основных электрических величин: тока, напряжения и сопротивления. Он показывает, как эти три величины являются взаимозависимыми на макроскопическом уровне.
Если бы было можно охарактеризовать закон Ома простыми словами, то наглядно это выглядело бы так:
Из закона Ома вытекает, что замыкать обычную осветительную сеть проводником малого сопротивления опасно. Сила тока окажется настолько большой, что это может иметь тяжелые последствия.
Рассчитать силу тока, проходящую по медному проводу длиной 100 м, площадью поперечного сечения 0,5 мм2, если к концам провода приложено напряжение 12 B.
Задачка простая, заключается в нахождении сопротивления медной проволоки с последующим расчетом силы тока по формуле закона Ома для участка цепи. Приступим.
Сопротивление
Представьте, что есть труба, в которую затолкали камни. Вода, которая протекает по этой трубе, станет течь медленнее, потому что у нее появилось сопротивление. Точно также будет происходить с электрическим током.
Теперь сделаем «каменный участок» длиннее, то есть добавим еще камней. Воде будет еще сложнее течь.
Сделаем трубу шире, оставив количество камней тем же — воде полегчает, поток увеличится.
Теперь заменим шероховатые камни, которые мы набрали на стройке, на гладкие камушки из моря. Через них проходить тоже легче, а значит сопротивление уменьшается.
Электрический ток реагирует на эти параметры аналогичным образом: при удлинении проводника сопротивление увеличивается, при увеличении поперечного сечения (ширины) проводника сопротивление уменьшается, а если заменить материал — изменится в зависимости от материала.
Эту закономерность можно описать следующей формулой:
Единица измерения сопротивления — Ом. Названа в честь физика Георга Ома.
Площадь поперечного сечения проводника и удельное сопротивление содержат в своих единицах измерения мм^2. В таблице удельное сопротивление всегда дается в такой размерности, да и тонкий проводник проще измерять в мм^2. При умножении мм^2 сокращаются и мы получаем величину в СИ.
Но это не отменяет того, что каждую задачу нужно проверять на то, что там мм^2 в обеих величинах! Если это не так, то нужно свести не соответствующую величину к мм^2.
Знайте!СИ — международная система единиц. «Перевести в СИ» означает перевод всех величин в метры, килограммы, секунды и другие единицы измерения без приставок. Исключение составляет килограмм с приставкой «кило».
Таблица удельных сопротивлений различных материалов
Удельное сопротивление
Удельное сопротивление
Алюминий0,028Бронза0,095 – 0,1Висмут1,2Вольфрам0,05Железо0,1Золото0,023Иридий0,0474Константан ( сплав Ni-Cu + Mn)0,5Латунь0,025 – 0,108Магний0,045Манганин (сплав меди марганца и никеля – приборный)0,43 – 0,51Медь0,0175Молибден0,059Нейзильбер (сплав меди цинка и никеля)0,2Натрий0,047Никелин ( сплав меди и никеля)0,42Никель0,087Нихром ( сплав никеля хрома железы и марганца)1,05 – 1,4Олово0,12Платина0. 107Ртуть0,94Свинец0,22Серебро0,015Сталь0,103 – 0,137Титан0,6Хромаль1,3 – 1,5Цинк0,054Чугун0,5-1,0
Резистор
Все реальные проводники имеют сопротивление, но его стараются сделать незначительным. В задачах вообще используют словосочетание «идеальный проводник», а значит лишают его сопротивления.
Из-за того, что проводник у нас «кругом-бегом-такой-идеальный», чаще всего за сопротивление в цепи отвечает резистор. Это устройство, которое нагружает цепь сопротивлением.
Вот так резистор изображается на схемах:
В школьном курсе физики используют Европейское обозначение, поэтому запоминаем только его. Американское обозначение можно встретить, например, в программе Micro-Cap, в которой инженеры моделируют схемы.
Вот так резистор выглядит в естественной среде обитания:
Полосочки на нем показывают его сопротивление.
На сайте компании Ekits, которая занимается продажей электронных модулей, можно выбрать цвет резистора и узнать значение его сопротивления:
О том, зачем дополнительно нагружать сопротивлением цепь, мы поговорим в этой же статье чуть позже.
Реостат
Есть такие выключатели, которые крутишь, а они делают свет ярче-тусклее. В такой выключатель спрятан резистор с переменным сопротивлением — реостат.
Стрелка сверху — это ползунок. По сути, он отсекает ту часть резистора, которая находится от него справа. То есть, если мы двигаем ползунок вправо — мы увеличиваем длину резистора, а значит и сопротивление. И наоборот — двигаем влево и уменьшаем.
По формуле сопротивления это очень хорошо видно, так как длина проводника находится в числителе:
Закон Ома для участка цепи
С камушками в трубе все понятно, но не только же от них зависит сила, с которой поток воды идет по трубе — от насоса, которым мы эту воду качаем, тоже зависит. Чем сильнее качаем, тем больше течение. В электрической цепи функцию насоса выполняет источник тока.
Например, источником может быть гальванический элемент (привычная батарейка). Батарейка работает на основе химических реакций внутри нее. Эти реакции выделяют энергию, которая потом передается электрической цепи.
У любого источника обязательно есть полюса — «плюс» и «минус». Полюса — это его крайние положения, по сути клеммы, к которым присоединяется электрическая цепь. Собственно, ток как раз течет от «+» к «-».
У нас уже есть две величины, от которых зависит электрический ток в цепи — напряжение и сопротивление. Кажется, пора объединять их в закон.
Сила тока в участке цепи прямо пропорциональна напряжению на его концах и обратно пропорциональна его сопротивлению.
Математически его можно описать вот так:
Напряжение измеряется в Вольтах и показывает разницу между двумя точками цепи: от этой разницы зависит, насколько сильно будет течь ток — чем больше разница, тем выше напряжение и ток будет течь сильнее.
Сила тока измеряется в Амперах, а подробнее о ней вы можете прочитать в нашей статье
Давайте решим несколько задач на Закон Ома для участка цепи.
Найти силу тока в лампочке накаливания, если торшер включили в сеть напряжением 220 В, а сопротивление нити накаливания равно 880 Ом.
Возьмем закон Ома для участка цепи:
I = U/R
I = 220/880 = 0,25 А
Ответ: сила тока, проходящего через лампочку, равна 0,25 А
Давайте усложним задачу. И найдем силу тока, знаю все параметры для вычисления сопротивления и напряжение.
Найти силу тока в лампочке накаливания, если торшер включили в сеть напряжением 220 В, а длина нити накаливания равна 0,5 м, площадь поперечного сечения 0,01 мм^2, а удельное сопротивление нити равно 1,05 Ом*мм^2/м.
Сначала найдем сопротивление проводника.
R = ρ l/S
Площадь дана в мм^2, а удельное сопротивления тоже содержит мм^2 в размерности.
Это значит, что можно подставлять значения без перевода в СИ:
R = 1,05*0,5/0,01 = 52,5 Ом
Теперь возьмем закон Ома для участка цепи:
I = U/R
I = 220/52,5 ≃ 4,2 А
Ответ: сила тока, проходящего через лампочку, приблизительно равна 4,2 А
А теперь совсем усложним! Определим материал, из которого изготовлена нить накаливания.
Из какого материала изготовлена нить накаливания лампочки, если настольная лампа включена в сеть напряжением 220 В, длина нити равна 0,5 м, площадь ее поперечного сечения равна 0,01 мм^2, а сила тока в цепи — 8,8 А
Возьмем закон Ома для участка цепи и выразим из него сопротивление:
I = U/R
R = U/I
Подставим значения и найдем сопротивление нити:
R = 220/8,8 = 25 Ом
Теперь возьмем формулу сопротивления и выразим из нее удельное сопротивление материала:
R = ρ l/S
ρ = RS/l
Подставим значения и получим:
ρ = 25*0,01/0,5 = 0,5 Ом*мм^2/м
Обратимся к таблице удельных сопротивлений материалов, чтобы выяснить, из какого материала сделана эта нить накаливания.
Закон Ома для полной цепи
Мы разобрались с законом Ома для участка цепи. А теперь давайте узнаем, что происходит, если цепь полная: у нее есть источник, проводники, резисторы и другие элементы.
В таком случае вводится Закон Ома для полной цепи: сила тока в полной цепи равна отношению ЭДС цепи к ее полному сопротивлению.
Так, стоп. Слишком много незнакомых слов — разбираемся по-порядку.
Что такое ЭДС и откуда она берется
ЭДС расшифровывается, как электродвижущая сила. Обозначается греческой буквой ε и измеряется, как и напряжение, в Вольтах.
Химическая реакция внутри гальванического элемента (это синоним батарейки) происходит с выделением энергии в электрическую цепь. Именно эта энергия заставляет частицы двигаться по проводнику.
Зачастую напряжение и ЭДС приравнивают и говорят, что это одно и то же. Формально, это не так, но при решении задач чаще всего и правда нет разницы, так как эти величины обе измеряются в Вольтах и определяют очень похожие по сути своей процессы.
В виде формулы Закон Ома для полной цепи будет выглядеть следующим образом:
Любой источник не идеален. В задачах это возможно («источник считать идеальным», вот эти вот фразочки), но в реальной жизни — точно нет. В связи с этим у источника есть внутреннее сопротивление, которое мешает протеканию тока.
Решим задачу на полную цепь.
Найти силу тока в полной цепи, состоящей из одного резистора сопротивлением 3 Ом и источником с ЭДС равной 4 В и внутренним сопротивлением 1 Ом
Возьмем закон Ома для полной цепи:
I = ε/(R + r)
I = 4/(3+1) = 1 A
Ответ: сила тока в цепи равна 1 А.
Когда «сопротивление бесполезно»
Электрический ток — умный и хитрый парень. Если у него есть возможность обойти резистор и пойти по идеальному проводнику без сопротивления, он это сделает. При этом с резисторами просто разных номиналов это не сработает: он не пойдет просто через меньшее сопротивление, а распределится согласно закону Ома — больше тока пойдет туда, где сопротивление меньше, и наоборот.
А вот на рисунке ниже сопротивление цепи равно нулю, потому что ток через резистор не пойдет.
Ток идет по пути наименьшего сопротивления.
Теперь давайте посмотрим на закон Ома для участка цепи еще раз.
Подставим сопротивление, равное 0. Получается, что знаменатель равен нулю, а на математике говорят, что на ноль делить нельзя. Но мы вам раскроем страшную тайну, только не говорите математикам: на ноль делить можно. Если совсем упрощать такое сложное вычисление (а именно потому что оно сложное, мы всегда говорим, что его нельзя производить), то получится бесконечность.
I = U/0 = ∞
Такой случай называют коротким замыканием — когда величина силы тока настолько велика, что можно устремить ее к бесконечности. В таких ситуациях мы видим искру, бурю, безумие — и все ломается.
Это происходит, потому что две точки цепи имеют между собой напряжение (то есть между ними есть разница). Это как если вдоль реки неожиданно появляется водопад. Из-за этой разницы возникает искра, которую можно избежать, поставив в цепь резистор.
Именно во избежание коротких замыканий нужно дополнительное сопротивление в цепи.
Формула Закона Джоуля-Ленца
Величину резистора для изготовления блока нагрузки для блока питания компьютера мы рассчитали, но нужно еще определить какой резистор должен быть мощности? Тут поможет другой закон физики, который, независимо друг от друга открыли одновременно два ученых физика. В 1841 году Джеймс Джоуль, а в 1842 году Эмиль Ленц. Этот закон и назвали в их честь – Закон Джоуля-Ленца.
Потребляемая нагрузкой мощность прямо пропорциональна приложенной величине напряжения и протекающей силе тока. Другими словами, при изменении величины напряжения и тока будет пропорционально будет изменяться и потребляемая мощность.
где P – мощность, измеряется в ваттах и обозначается Вт;U – напряжение, измеряется в вольтах и обозначается буквой В;I – сила ток, измеряется в амперах и обозначается буквой А.
Зная напряжения питания и силу тока, потребляемую электроприбором, можно по формуле определить, какую он потребляет мощность. Достаточно ввести данные в окошки ниже приведенного онлайн калькулятора.
Закон Джоуля-Ленца позволяет также узнать силу тока, потребляемую электроприбором зная его мощность и напряжение питания. Величина потребляемого тока необходима, например, для выбора сечения провода при прокладке электропроводки или для расчета номинала.
Например, рассчитаем потребляемый ток стиральной машины. По паспорту потребляемая мощность составляет 2200 Вт, напряжение в бытовой электросети составляет 220 В. Подставляем данные в окошки калькулятора, получаем, что стиральная машина потребляет ток величиной 10 А.
Еще один пример, Вы решили в автомобиле установить дополнительную фару или усилитель звука. Зная потребляемую мощность устанавливаемого электроприбора легко рассчитать потребляемый ток и правильно подобрать сечение провода для подключения к электропроводке автомобиля. Допустим, дополнительная фара потребляет мощность 100 Вт (мощность установленной в фару лампочки), бортовое напряжение сети автомобиля 12 В. Подставляем значения мощности и напряжения в окошки калькулятора, получаем, что величина потребляемого тока составит 8,33 А.
Разобравшись всего в двух простейших формулах, Вы легко сможете рассчитать текущие по проводам токи, потребляемую мощность любых электроприборов – практически начнете разбираться в основах электротехники.
Преобразованные формулы Закона Ома и Джоуля-Ленца
Встретил в Интернете картинку в виде круглой таблички, в которой удачно размещены формулы Закона Ома и Джоуля-Ленца и варианты математического преобразования формул. Табличка представляет собой не связанные между собой четыре сектора и очень удобна для практического применения
По таблице легко выбрать формулу для расчета требуемого параметра электрической цепи по двум другим известным. Например, нужно определить ток потребления изделием по известной мощности и напряжению питающей сети. По таблице в секторе тока видим, что для расчета подойдет формула I=P/U.
А если понадобится определить напряжение питающей сети U по величине потребляемой мощности P и величине тока I, то можно воспользоваться формулой левого нижнего сектора, подойдет формула U=P/I.
Подставляемые в формулы величины должны быть выражены в амперах, вольтах, ваттах или Омах.
Применение закона Ома на практике
На практике часто приходится определять не силу тока I, а величину сопротивления R. Преобразовав формулу Закона Ома, можно рассчитать величину сопротивления R, зная протекающий ток I и величину напряжения U.
Величину сопротивления может понадобится рассчитать, например, при изготовлении блока нагрузок для проверки блока питания компьютера. На корпусе блока питания компьютера обычно есть табличка, в которой приведен максимальный ток нагрузки по каждому напряжению. Достаточно в поля калькулятора ввести данные величины напряжения и максимальный ток нагрузки и в результате вычисления получим величину сопротивления нагрузки для данного напряжения. Например, для напряжения +5 В при максимальной величине тока 20 А, сопротивление нагрузки составит 0,25 Ом.
Таблица-шпаргалка
Используя закон Ома для участка цепи, а также формулу для мощности электрического тока: P = U*I – я подготовил для вас полезную таблицу-шпаргалку, которая позволяет соотносить между собой сопротивление (R), силу тока (I), напряжение (U) и мощность электрического тока (P). Будет точно полезно не только школьникам!
Известные величиныR (сопротивление)I (сила тока)U (напряжение)P (мощность)Ток и сопротивлениеU = I × RP = I2 × RНапряжение и токR = U / IP = U × IМощность и токR = P / I2U = P / IНапряжение и сопротивлениеI = U / RP = U2 / RМощность и сопротивлениеI = P / RНапряжение и мощностьR = U2 / RI = P / U
Последовательное и параллельное включение элементов
Для элементов электрической цепи (участка цепи) характерным моментом является последовательное либо параллельное соединение. Соответственно, каждый вид соединения сопровождается разным характером течения тока и подводкой напряжения. На этот счёт закон Ома также применяется по-разному, в зависимости от варианта включения элементов.
Цепь последовательно включенных резистивных элементов
Применительно к последовательному соединению (участку цепи с двумя компонентами) используется формулировка:
- I = I1= I2 ;
- U = U1+ U2 ;
- R = R1+ R2
Такая формулировка явно демонстрирует, что, независимо от числа последовательно соединенных резистивных компонентов, ток, текущий на участке цепи, не меняет значения. Величина напряжения, приложенного к действующим резистивным компонентам схемы, является суммой и составляет в целом значение источника ЭДС.
При этом напряжение на каждом отдельном компоненте равно: Ux = I * Rx. Общее сопротивление следует рассматривать как сумму номиналов всех резистивных компонентов цепи.
Цепь параллельно включенных резистивных элементов
На случай, когда имеет место параллельное включение резистивных компонентов, справедливой относительно закона немецкого физика Ома считается формулировка:
- I = I1+ I2 … ;
- U = U1= U2 … ;
- 1 / R = 1 / R1+ 1 / R2 + …
Не исключаются варианты составления схемных участков «смешанного» вида, когда используется параллельное и последовательное соединение. Для таких вариантов расчет обычно ведется изначальным расчетом резистивного номинала параллельного соединения. Затем к полученному результату добавляется номинал резистора, включенного последовательно.
Интегральная и дифференциальная формы закона
Все вышеизложенные моменты с расчетами применимы к условиям, когда в составе электрических схем используются проводники, так сказать, «однородной» структуры. Между тем на практике нередко приходится сталкиваться с построением схематики, где на различных участках структура проводников меняется. К примеру, используются провода большего сечения или, напротив, меньшего, сделанные на основе разных материалов.
Для учёта таких различий существует вариация, так называемого, «дифференциально-интегрального закона Ома». Для бесконечно малого проводника рассчитывается уровень плотности тока в зависимости от напряженности и величины удельной проводимости.
Под дифференциальный расчет берется формула: J = ό * E. Для интегрального расчета, соответственно, формулировка: I * R = φ1 – φ2 + έ Однако эти примеры скорее уже ближе к школе высшей математики и в реальной практике простого электрика фактически не применяются.