Опыт с катушкой и магнитом
Взаимодействие движущегося магнита и катушки, намотанной из проводника, порождает электрический ток. Магнит при этом обязательно должен двигаться. Простое наличие неподвижного магнита вблизи катушки электрического тока не производит. Более того, при введении магнита в катушку в цепи возникает электрический ток одного направления (стрелка гальванометра отклоняется, например, вправо); при выведении магнита из катушки стрелка отклоняется в противоположную сторону. Таким образом, характер тока зависит от скорости и направления движения магнита, а также от того, каким полюсом он вставляется в катушку.
Возникающий при движении магнита внутри катушки или близ ее ток называется индукционным (самонаводящимся).
Наблюдения Фарадея за взаимодействием магнита и катушки с проводником заложили начала современной электротехники. На этом принципе работают современные электродвигатели постоянного тока (см. пример ниже).
Опыт с двумя катушками
Опыт с двумя катушками заключался в том, что по одной из них пропускали ток, к другой был подключен гальванометр. В момент начала или окончания пропускания тока по первой катушке стрелка гальванометра, подключенного ко второй, колебалась. Этот опыт Фарадея показывал, что не только магнетизм можно превратить в электричество, но и электричество в магнетизм. Переменный ток, пропускаемый через одну из двух расположенных близко друг к другу катушек, превращал ее в магнит, наводящий ток в соседней. Характеристики магнитного поля (полярность, интенсивность) зависели от силы пропускаемого тока.
На принципе взаимодействия катушек с переменным током работают современные трансформаторы, применяемые в электронике и электротехнике.
Электродвижущая сила
Эксперименты Фарадея и его последователей показали, что в контуре электрического проводника при изменении магнитного потока возникает электродвижущая сила (ЭДС), выражаемая формулой:
Знак минус здесь связан с правилом Ленца, по которому определяется направление индукционного тока.
Одно из практических применений явление электромагнитной индукции нашло в конструировании электродвигателей и электрогенераторов. Ток можно вырабатывать в системах, где магнит вращается в токопроводящем контуре или, напротив, контур в неподвижном магнитном поле. Рассмотрим источник переменной ЭДС.
Вращаясь в равномерном магнитном поле, рамка пересекает силовые линии его магнитного поля. В каждой из ее сторон, параллельных оси вращения, наводится ЭДС.
Стороны рамки, перпендикулярные оси вращения, не пересекают силовых линий и ЭДС не создают.
На противоположных сторонах рамки возникают противоположные по направлению ЭДС. Для определения направления силы используется правило правой руки: ладонь следует расположить так, чтобы она была обращена в сторону северного полюса магнита, а большой отогнутый палец совпадал с направлением движения той стороны рамки, в которой требуется определить направление ЭДС. Его укажут вытянутые пальцы руки.
Не трудно заметить, что на сторонах, параллельных оси вращения рамки, электродвижущие силы всегда складываются. При этом по мере вращения рамки направление общей ЭДС изменяется в ней на обратное, поскольку каждая из рабочих сторон рамки за один оборот проходит под разными полюсами магнита. Сила индуцируемого тока в сторонах рамки также изменяется по мере изменения скорости, с которой они пересекают линии магнитного поля. Когда плоскость рамки параллельна силовым линиям, скорость пересечения силовых линий сторонами и, следовательно, ЭДС максимальны.
Таким образом, при равномерном вращении рамки в ней будет индуктироваться ЭДС, периодически изменяющаяся как по величине, так и по направлению.
Электромагнитная индукция
Автор статьи — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев
Темы кодификатора ЕГЭ: явление электромагнитной индукции, магнитный поток, закон электромагнитной индукции Фарадея, правило Ленца.
Опыт Эрстеда показал, что электрический ток создаёт в окружающем пространстве магнитное поле. Майкл Фарадей пришёл к мысли, что может существовать и обратный эффект: магнитное поле, в свою очередь, порождает электрический ток.
Иными словами, пусть в магнитном поле находится замкнутый проводник; не будет ли в этом проводнике возникать электрический ток под действием магнитного поля?
Через десять лет поисков и экспериментов Фарадею наконец удалось этот эффект обнаружить. В 1831 году он поставил следующие опыты.
На одну и ту же деревянную основу были намотаны две катушки; витки второй катушки были проложены между витками первой и изолированы. Выводы первой катушки подключались к источнику тока, выводы второй катушки — к гальванометру (гальванометр — чувствительный прибор для измерения малых токов). Таким образом, получались два контура: «источник тока — первая катушка» и «вторая катушка — гальванометр».
Электрического контакта между контурами не было, только лишь магнитное поле первой катушки пронизывало вторую катушку.
При замыкании цепи первой катушки гальванометр регистрировал короткий и слабый импульс тока во второй катушке.
Когда по первой катушке протекал постоянный ток, никакого тока во второй катушке не возникало.
При размыкании цепи первой катушки снова возникал короткий и слабый импульс тока во второй катушке, но на сей раз в обратном направлении по сравнению с током при замыкании цепи.
Меняющееся во времени магнитное поле первой катушки порождает (или, как говорят, индуцирует) электрический ток во второй катушке. Этот ток называется индукционным током.
Если магнитное поле первой катушки увеличивается (в момент нарастания тока при замыкании цепи), то индукционный ток во второй катушке течёт в одном направлении.
Если магнитное поле первой катушки уменьшается (в момент убывания тока при размыкании цепи), то индукционный ток во второй катушке течёт в другом направлении.
Если магнитное поле первой катушки не меняется (постоянный ток через неё), то индукционного тока во второй катушке нет.
Обнаруженное явление Фарадей назвал электромагнитной индукцией (т. «наведение электричества магнетизмом»).
Для подтверждения догадки о том, что индукционный ток порождается переменным магнитным полем, Фарадей перемещал катушки друг относительно друга. Цепь первой катушки всё время оставалась замкнутой, по ней протекал постоянный ток, но за счёт перемещения (сближения или удаления) вторая катушка оказывалась в переменном магнитном поле первой катушки.
Гальванометр снова фиксировал ток во второй катушке. Индукционный ток имел одно направление при сближении катушек, и другое — при их удалении. При этом сила индукционного тока была тем больше, чем быстрее перемещались катушки.
Первая катушка была заменена постоянным магнитом. При внесении магнита внутрь второй катушки возникал индукционный ток. При выдвигании магнита снова появлялся ток, но в другом направлении. И опять-таки сила индукционного тока была тем больше, чем быстрее двигался магнит.
Эти и последующие опыты показали, что индукционный ток в проводящем контуре возникает во всех тех случаях, когда меняется «количество линий» магнитного поля, пронизывающих контур. Сила индукционного тока оказывается тем больше, чем быстрее меняется это количество линий. Направление тока будет одним при увеличении количества линий сквозь контур, и другим — при их уменьшении.
Замечательно, что для величины силы тока в данном контуре важна лишь скорость изменения количества линий. Что конкретно при этом происходит, роли не играет — меняется ли само поле, пронизывающее неподвижный контур, или же контур перемещается из области с одной густотой линий в область с другой густотой.
Такова суть закона электромагнитной индукции. Но, чтобы написать формулу и производить расчёты, нужно чётко формализовать расплывчатое понятие «количество линий поля сквозь контур».
Понятие магнитного потока как раз и является характеристикой количества линий магнитного поля, пронизывающих контур.
Для простоты мы ограничиваемся случаем однородного магнитного поля. Рассмотрим контур площади , находящийся в магнитном поле с индукцией.
Пусть сначала магнитное поле перпендикулярно плоскости контура (рис.
В этом случае магнитный поток определяется очень просто — как произведение индукции магнитного поля на площадь контура:
Теперь рассмотрим общий случай, когда вектор образует угол с нормалью к плоскости контура (рис.
Мы видим, что теперь сквозь контур «протекает» лишь перпендикулярная составляющая вектора магнитной индукции (а та составляющая, которая параллельна контуру, не «течёт» сквозь него). Поэтому, согласно формуле (1), имеем. Но , поэтому
Это и есть общее определение магнитного потока в случае однородного магнитного поля. Обратите внимание, что если вектор параллелен плоскости контура (то есть ), то магнитный поток становится равным нулю.
А как определить магнитный поток, если поле не является однородным? Укажем лишь идею. Поверхность контура разбивается на очень большое число очень маленьких площадок, в пределах которых поле можно считать однородным. Для каждой площадки вычисляем свой маленький магнитный поток по формуле (2), а затем все эти магнитные потоки суммируем.
Единицей измерения магнитного потока является вебер (Вб). Как видим,
Вб = Тл · м = В · с. (3)
Почему же магнитный поток характеризует «количество линий» магнитного поля, пронизывающих контур? Очень просто. «Количество линий» определяется их густотой (а значит, величиной — ведь чем больше индукция, тем гуще линии) и «эффективной» площадью, пронизываемой полем (а это есть не что иное, как ). Но множители и как раз и образуют магнитный поток!
Теперь мы можем дать более чёткое определение явления электромагнитной индукции, открытого Фарадеем.
Электромагнитная индукция — это явление возникновения электрического тока в замкнутом проводящем контуре при изменении магнитного потока, пронизывающего контур.
Каков механизм возникновения индукционного тока? Это мы обсудим позже. Пока ясно одно: при изменении магнитного потока, проходящего через контур, на свободные заряды в контуре действуют некоторые силы — сторонние силы, вызывающие движение зарядов.
Как мы знаем, работа сторонних сил по перемещению единичного положительного заряда вокруг контура называется электродвижущей силой (ЭДС):. В нашем случае, когда меняется магнитный поток сквозь контур, соответствующая ЭДС называется ЭДС индукции и обозначается.
Итак, ЭДС индукции — это работа сторонних сил, возникающих при изменении магнитного потока через контур, по перемещению единичного положительного заряда вокруг контура.
Природу сторонних сил, возникающих в данном случае в контуре, мы скоро выясним.
Сила индукционного тока в опытах Фарадея оказывалась тем больше, чем быстрее менялся магнитный поток через контур.
Если за малое время изменение магнитного потока равно , то скорость изменения магнитного потока — это дробь (или, что тоже самое, производная магнитного потока по времени).
Опыты показали, что сила индукционного тока прямо пропорциональна модулю скорости изменения магнитного потока:
Модуль поставлен для того, чтобы не связываться пока с отрицательными величинами (ведь при убывании магнитного потока будет ). Впоследствии мы это модуль снимем.
Из закона Ома для полной цепи мы в то же время имеем:. Поэтому ЭДС индукции прямо пропорциональна скорости изменения магнитного потока:
ЭДС измеряется в вольтах. Но и скорость изменения магнитного потока также измеряется в вольтах! Действительно, из (3) мы видим, что Вб/с = В. Стало быть, единицы измерения обеих частей пропорциональности (4) совпадают, поэтому коэффициент пропорциональности — величина безразмерная. В системе СИ она полагается равной единице, и мы получаем:
Это и есть закон электромагнитной индукции или закон Фарадея. Дадим его словесную формулировку.
Закон электромагнитной индукции Фарадея. При изменении магнитного потока, пронизывающего контур, в этом контуре возникает ЭДС индукции, равная модулю скорости изменения магнитного потока.
Магнитный поток, изменение которого приводит к появлению индукционного тока в контуре, мы будем называть внешним магнитным потоком. А само магнитное поле, которое создаёт этот магнитный поток, мы будем называть внешним магнитным полем.
Зачем нам эти термины? Дело в том, что индукционный ток, возникающий в контуре, создаёт своё собственное магнитное поле, которое по принципу суперпозиции складывается с внешним магнитным полем.
Соответственно, наряду с внешним магнитным потоком через контур будет проходить собственный магнитный поток, создаваемый магнитным полем индукционного тока.
Оказывается, эти два магнитных потока — собственный и внешний — связаны между собой строго определённым образом.
Правило Ленца. Индукционный ток всегда имеет такое направление, что собственный магнитный поток препятствует изменению внешнего магнитного потока.
Правило Ленца позволяет находить направление индукционного тока в любой ситуации.
Рассмотрим некоторые примеры применения правила Ленца.
Предположим, что контур пронизывается магнитным полем, которое возрастает со временем (рис. (3)). Например, мы приближаем снизу к контуру магнит, северный полюс которого направлен в данном случае вверх, к контуру.
Магнитный поток через контур увеличивается. Индукционный ток будет иметь такое направление, чтобы создаваемый им магнитный поток препятствовал увеличению внешнего магнитного потока. Для этого магнитное поле, создаваемое индукционным током, должно быть направлено против внешнего магнитного поля.
Индукционный ток течёт против часовой стрелки, если смотреть со стороны создаваемого им магнитного поля. В данном случае ток будет направлен по часовой стрелке, если смотреть сверху, со стороны внешнего магнитного поля, как и показано на (рис. (3)).
Рис. Магнитный поток возрастает
Теперь предположим, что магнитное поле, пронизывающее контур, уменьшается со временем (рис. Например, мы удаляем магнит вниз от контура, а северный полюс магнита направлен на контур.
Рис. Магнитный поток убывает
Магнитный поток через контур уменьшается. Индукционный ток будет иметь такое направление, чтобы его собственный магнитный поток поддерживал внешний магнитный поток, препятствуя его убыванию. Для этого магнитное поле индукционного тока должно быть направлено в ту же сторону , что и внешнее магнитное поле.
В этом случае индукционный ток потечёт против часовой стрелки, если смотреть сверху, со стороны обоих магнитных полей.
Итак, приближение или удаление магнита приводит к появлению в контуре индукционного тока, направление которого определяется правилом Ленца. Но ведь магнитное поле действует на ток! Появится сила Ампера, действующая на контур со стороны поля магнита. Куда будет направлена эта сила?
Если вы хотите хорошо разобраться в правиле Ленца и в определении направления силы Ампера, попробуйте ответить на данный вопрос самостоятельно. Это не очень простое упражнение и отличная задача для С1 на ЕГЭ. Рассмотрите четыре возможных случая.
Магнит приближаем к контуру, северный полюс направлен на контур. Магнит удаляем от контура, северный полюс направлен на контур. Магнит приближаем к контуру, южный полюс направлен на контур. Магнит удаляем от контура, южный полюс направлен на контур.
Не забывайте, что поле магнита не однородно: линии поля расходятся от северного полюса и сходятся к южному. Это очень существенно для определения результирующей силы Ампера. Результат получается следующий.
Если приближать магнит, то контур отталкивается от магнита. Если удалять магнит, то контур притягивается к магниту. Таким образом, если контур подвешен на нити, то он всегда будет отклоняться в сторону движения магнита, словно следуя за ним. Расположение полюсов магнита при этом роли не играет.
Уж во всяком случае вы должны запомнить этот факт — вдруг такой вопрос попадётся в части А1
Результат этот можно объяснить и из совершенно общих соображений — при помощи закона сохранения энергии.
Допустим, мы приближаем магнит к контуру. В контуре появляется индукционный ток. Но для создания тока надо совершить работу! Кто её совершает? В конечном счёте — мы, перемещая магнит. Мы совершаем положительную механическую работу, которая преобразуется в положительную работу возникающих в контуре сторонних сил, создающих индукционный ток.
Итак, наша работа по перемещению магнита должна быть положительна. Это значит, что мы, приближая магнит, должны преодолевать силу взаимодействия магнита с контуром, которая, стало быть, является силой отталкивания.
Теперь удаляем магнит. Повторите, пожалуйста, эти рассуждения и убедитесь, что между магнитом и контуром должна возникнуть сила притяжения.
Выше мы обещали снять модуль в законе Фарадея (5). Правило Ленца позволяет это сделать. Но сначала нам нужно будет договориться о знаке ЭДС индукции — ведь без модуля, стоящего в правой части (5), величина ЭДС может получаться как положительной, так и отрицательной.
Прежде всего, фиксируется одно из двух возможных направлений обхода контура. Это направление объявляется положительным. Противоположное направление обхода контура называется, соответственно, отрицательным. Какое именно направление обхода мы берём в качестве положительного, роли не играет — важно лишь сделать этот выбор.
Магнитный поток через контур считается положительным , если магнитное поле, пронизывающее контур, направлено туда, глядя откуда обход контура в положительном направлении совершается против часовой стрелки. Если же с конца вектора магнитной индукции положительное направление обхода видится по часовой стрелке, то магнитный поток считается отрицательным.
ЭДС индукции считается положительной , если индукционный ток течёт в положительном направлении. В этом случае направление сторонних сил, возникающих в контуре при изменении магнитного потока через него, совпадает с положительным направлением обхода контура.
Наоборот, ЭДС индукции считается отрицательной , если индукционный ток течёт в отрицательном направлении. Сторонние силы в данном случае также будут действовать вдоль отрицательного направления обхода контура.
Итак, пусть контур находится в магнитном поле. Фиксируем направление положительного обхода контура. Предположим, что магнитное поле направлено туда, глядя откуда положительный обход совершается против часовой стрелки. Тогда магнитный поток положителен:.
Предположим, далее, что магнитный поток увеличивается. Согласно правилу Ленца индукционный ток потечёт в отрицательном направлении (рис.
Рис. Магнитный поток возрастает
Стало быть, в данном случае имеем. Знак ЭДС индукции оказался противоположен знаку скорости изменения магнитного потока. Проверим это в другой ситуации.
А именно, предположим теперь, что магнитный поток убывает. По правилу Ленца индукционный ток потечёт в положительном направлении. Стало быть, (рис.
Рис. Магнитный поток возрастает
Таков в действительности общий факт: при нашей договорённости о знаках правило Ленца всегда приводит к тому, что знак ЭДС индукции противоположен знаку скорости изменения магнитного потока :
Тем самым ликвидирован знак модуля в законе электромагнитной индукции Фарадея.
Рассмотрим неподвижный контур, находящийся в переменном магнитном поле. Каков же механизм возникновения индукционного тока в контуре? А именно, какие силы вызывают движение свободных зарядов, какова природа этих сторонних сил?
Пытаясь ответить на эти вопросы, великий английский физик Максвелл открыл фундаментальное свойство природы: меняющееся во времени магнитное поле порождает поле электрическое. Именно это электрическое поле и действует на свободные заряды, вызывая индукционный ток.
Линии возникающего электрического поля оказываются замкнутыми, в связи с чем оно было названо вихревым электрическим полем. Линии вихревого электрического поля идут вокруг линий магнитного поля и направлены следующим образом.
Пусть магнитное поле увеличивается. Если в нём находится проводящий контур, то индукционный ток потечёт в соответствии с правилом Ленца — по часовой стрелке, если смотреть с конца вектора. Значит, туда же направлена и сила, действующая со стороны вихревого электрического поля на положительные свободные заряды контура; значит, именно туда направлен вектор напряжённости вихревого электрического поля.
Итак, линии напряжённости вихревого электрического поля направлены в данном случае по часовой стрелке (смотрим с конца вектора , (рис.
Рис. Вихревое электрическое поле при увеличении магнитного поля
Наоборот, если магнитное поле убывает, то линии напряжённости вихревого электрического поля направлены против часовой стрелки (рис.
Рис. Вихревое электрическое поле при уменьшении магнитного поля
Теперь мы можем глубже понять явление электромагнитной индукции. Суть его состоит именно в том, что переменное магнитное поле порождает вихревое электрическое поле. Данный эффект не зависит от того, присутствует ли в магнитном поле замкнутый проводящий контур или нет; с помощью контура мы лишь обнаруживаем это явление, наблюдая индукционный ток.
Вихревое электрическое поле по некоторым свойствам отличается от уже известных нам электрических полей: электростатического поля и стационарного поля зарядов, образующих постоянный ток.
Линии вихревого поля замкнуты, тогда как линии электростатического и стационарного полей начинаются на положительных зарядах и оканчиваются на отрицательных. Вихревое поле непотенциально: его работа перемещению заряда по замкнутому контуру не равна нулю. Иначе вихревое поле не могло бы создавать электрический ток! В то же время, как мы знаем, электростатическое и стационарное поля являются потенциальными.
Итак, ЭДС индукции в неподвижном контуре — это работа вихревого электрического поля по перемещению единичного положительного заряда вокруг контура.
Пусть, например, контур является кольцом радиуса и пронизывается однородным переменным магнитным полем. Тогда напряжённость вихревого электрического поля одинакова во всех точках кольца. Работа силы , с которой вихревое поле действует на заряд , равна:
Следовательно, для ЭДС индукции получаем:
Если проводник перемещается в постоянном магнитном поле, то в нём также появляется ЭДС индукции. Однако причиной теперь служит не вихревое электрическое поле (оно не возникает — ведь магнитное поле постоянно), а действие силы Лоренца на свободные заряды проводника.
Рассмотрим ситуацию, которая часто встречается в задачах. В горизонтальной плоскости расположены параллельные рельсы, расстояние между которыми равно. Рельсы находятся в вертикальном однородном магнитном поле. По рельсам движется тонкий проводящий стержень со скоростью ; он всё время остаётся перпендикулярным рельсам (рис.
Рис. Движение проводника в магнитном поле
Возьмём внутри стержня положительный свободный заряд. Вследствие движения этого заряда вместе со стержнем со скоростью на заряд будет действовать сила Лоренца:
Направлена эта сила вдоль оси стержня, как показано на рисунке (убедитесь в этом сами — не забывайте правило часовой стрелки или левой руки!).
Сила Лоренца играет в данном случае роль сторонней силы: она приводит в движение свободные заряды стержня. При перемещении заряда от точки к точке наша сторонняя сила совершит работу:
(Длину стержня мы также считаем равной. ) Стало быть, ЭДС индукции в стержне окажется равной:
Таким образом, стержень аналогичен источнику тока с положительной клеммой и отрицательной клеммой. Внутри стержня за счёт действия сторонней силы Лоренца происходит разделение зарядов: положительные заряды двигаются к точке , отрицательные — к точке.
Допустим сначала,что рельсы непроводят ток. Тогда движение зарядов в стержне постепенно прекратится. Ведь по мере накопления положительных зарядов на торце и отрицательных зарядов на торце будет возрастать кулоновская сила, с которой положительный свободный заряд отталкивается от и притягивается к — и в какой-то момент эта кулоновская сила уравновесит силу Лоренца. Между концами стержня установится разность потенциалов, равная ЭДС индукции (7).
Теперь предположим, что рельсы и перемычка являются проводящими. Тогда в цепи возникнет индукционный ток; он пойдёт в направлении (от «плюса источника» к «минусу» N). Предположим, что сопротивление стержня равно (это аналог внутреннего сопротивления источника тока), а сопротивление участка равно (сопротивление внешней цепи). Тогда сила индукционного тока найдётся по закону Ома для полной цепи:
Замечательно, что выражение (7) для ЭДС индукции можно получить также с помощью закона Фарадея. Сделаем это. За время наш стержень проходит путь и занимает положение (рис. Площадь контура возрастает на величину площади прямоугольника :
Магнитный поток через контур увеличивается. Приращение магнитного потока равно:
Скорость изменения магнитного потока положительна и равна ЭДС индукции:
Мы получили тот же самый результат, что и в (7). Направление индукционного тока, заметим, подчиняется правилу Ленца. Действительно, раз ток течёт в направлении , то его магнитное поле направлено противоположно внешнему полю и, стало быть, препятствует возрастанию магнитного потока через контур.
На этом примере мы видим, что в ситуациях, когда проводник движется в магнитном поле, можно действовать двояко: либо с привлечением силы Лоренца как сторонней силы, либо с помощью закона Фарадея. Результаты будут получаться одинаковые.
Как решать задачи
Закон Фарадея лежит в основе практически всей электрической промышленности. Предлагаем рассмотреть примеры решения задач, где встречается это физическое явление.
Надеемся, наша статья была вам полезна, и с заданиями по физике, касающимися этой темы, вы справитесь без труда. Но если возникнут проблемы, то в ФениксХелп вам всегда помогут.
История развития и опыты Фарадея
До середины 19 века считалось, что электрическое и магнитное поля не имеют связи, и природа их существования была иной. Но М. Фарадей был уверен в общности этих полей и их свойств. Открытое им явление электромагнитной индукции впоследствии стало основой для построения генераторов всех электростанций. Благодаря этому открытию человеческие знания об электромагнетизме шагнули вперед.
Фарадей провел следующий эксперимент: он замкнул цепь в катушке I, и магнитное поле вокруг нее увеличилось. Кроме того, индукционные линии этого магнитного поля проходили через катушку II, в которой возник индукционный ток.
Рис. Схема эксперимента Фарадея
Фактически, одновременно с Фарадеем, но независимо от него, это явление открыл другой ученый, Джозеф Генри. Однако Фарадей опубликовал свое исследование раньше. Таким образом, Майкл Фарадей стал автором закона электромагнитной индукции.
Независимо от количества проведенных Фарадеем экспериментов одно условие оставалось неизменным: для образования индукционного тока важно изменять магнитный поток, входящий в замкнутую проводящую цепь (катушку).
Закон Фарадея
Явление электромагнитной индукции определяется появлением электрического тока в электрически проводящей замкнутой цепи при изменении магнитного потока через область этой цепи.
Основной закон Фарадея состоит в том, что электродвижущая сила (ЭДС) прямо пропорциональна скорости изменения магнитного потока.
Формула закона электромагнитной индукции Фарадея выглядит следующим образом:
Рис. Формула закона электромагнитной индукции
И если сама формула, основанная на приведенных выше пояснениях, вопросов не вызывает, то знак «-» может вызвать сомнения. Оказывается, существует правило Ленца, русского ученого, проводившего свои исследования на основе постулатов Фарадея. Согласно Ленцу, знак «-» указывает направление возникающей ЭДС, то есть индукционный ток направлен таким образом, что магнитный поток, который он создает через область, ограниченную цепью, стремится предотвратить изменение потока, которое вызывает такой ток.
Основные понятия и законы электростатики
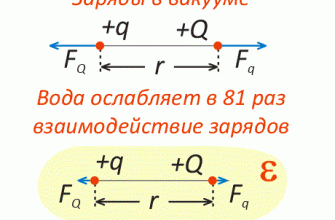
Закон Кулона:
сила взаимодействия двух неподвижных точечных зарядов в вакууме прямо пропорциональна произведению модулей заряда и обратно пропорциональна квадрату их расстояния:
Коэффициент пропорциональности в этом законе
Потенциал электрического поля – это отношение потенциальной энергии заряда в поле к этому заряду:
Записываем полевые работы в виде
Здесь U = ϕ1 – ϕ2 – разность потенциалов в начальной и конечной точках траектории. Разность потенциалов также называется напряжением
Часто наряду с понятием «разность потенциалов» вводится понятие «потенциал определенной точки поля». Потенциал точки указывает разность потенциалов между данной точкой и предварительно выбранной точкой в поле. Эту точку можно выбирать бесконечно, поэтому говорят о потенциале относительной бесконечности. Полевой потенциал точечного заряда рассчитывается по формуле
Проекция напряженности электрического поля на ось и потенциал связаны соотношением
Электроёмкость. Конденсаторы. Энергия электрического поля
Электрическая емкость тела называется величиной отношения
Формула для расчета емкости плоского конденсатора:
где S – площадь пластин, d – расстояние между ними. Конденсаторы можно подключать к батареям. При параллельном подключении емкость батареи C равна сумме емкостей конденсаторов:
Разности потенциалов между пластинами одинаковы, а заряды прямо пропорциональны емкостям. При последовательном подключении обратная величина емкости аккумулятора равна сумме обратных емкостей, включенных в аккумулятор:
Заряды конденсаторов одинаковы, а разность потенциалов обратно пропорциональна емкостям. Заряженный конденсатор обладает энергией. Энергию заряженного конденсатора можно рассчитать по одной из следующих формул:
Основные понятия и законы постоянного тока
Электрический ток – это прямое движение электрических зарядов. В разных веществах переносчиками заряда выступают элементарные частицы разного знака. Направление движения положительных зарядов считается положительным направлением тока. Электрический ток количественно характеризуется его силой. Это заряд, прошедший за единицу времени через поперечное сечение проводника:
Закон Ома для участка цепи:
Коэффициент пропорциональности R, называемый электрическим сопротивлением, является характеристикой проводника R = Ом. Сопротивление проводника зависит от его геометрии и свойств материала:
где l – длина проводника, – удельное сопротивление, S – площадь поперечного сечения это характеристика материала и его состояния. ρ = Ом · м. Проводники можно подключать последовательно. Сопротивление этого соединения определяется как сумма сопротивлений:
При параллельном подключении сопротивление, обратное сопротивлению, равно сумме обратных сопротивлений:
Чтобы электрический ток протекал в цепи в течение длительного времени, источники тока должны содержаться в цепи. Количественно источники тока характеризуются своей электродвижущей силой (ЭДС). Это отношение работы, совершаемой внешними силами при передаче электрических зарядов по замкнутой цепи, к величине перенесенного заряда:
Если к клеммам источника тока подключить сопротивление нагрузки R, то в образовавшейся замкнутой цепи будет течь ток, силу которого можно рассчитать по формуле
Это соотношение называется законом Ома для замкнутой цепи. Электрический ток, протекающий по проводникам, нагревает их во время работы
где t – время, I – сила тока, U – разность потенциалов, q – прошедший заряд. Закон Джоуля-Ленца:
Основные понятия и законы магнитостатики
Характеристикой магнитного поля является магнитная индукция ➛B. Поскольку это вектор, необходимо определить как направление этого вектора, так и его величину. Направление вектора магнитной индукции связано с ориентационным действием магнитного поля на магнитную стрелку. Направление вектора магнитной индукции берется от южного полюса S к северному полюсу N магнитной стрелки, которая свободно установлена в магнитном поле. Направление вектора магнитной индукции прямого проводника с токами можно определить с помощью правила подвеса:
если направление поступательного перемещения кардана совпадает с направлением тока в проводнике, то направление вращения ручки карданного подвеса совпадает с направлением вектора магнитной индукции. Величина вектора магнитной индукции – это отношение максимальной силы, действующей со стороны магнитного поля на участок проводника с током, к произведению силы тока на длину этого участка:
Единица магнитной индукции называется тесла (1 Тл)
Магнитным потоком через поверхность контура площадью S называют величину, равную произведению модуля вектора магнитной индукции на площадь этой поверхности и на косинус угла между вектором магнитной индукции ➛ B и нормаль к поверхности ➛n:
Единица измерения магнитного потока – Вебер (1 Вб). На проводник с током, помещенный в магнитное поле, действует сила Ампера
Закон Ампера:
на участок проводника с током силы I и длиной l, помещенный в однородное магнитное поле с индукцией ➛B, действует сила, модуль которой равен произведению модуля вектора магнитной индукции на интенсивность ток, длина участка проводника в магнитном поле и синус угла между направлением вектора ➛B и проводником с током:
Направление силы Ампера определяется по правилу левой руки:
если левая рука расположена таким образом, что составляющая вектора магнитной индукции, перпендикулярная проводнику, входит в ладонь и четыре вытянутых пальца будут указывать направление тока, то большой палец, согнутый под углом 90 °, будет указывать направление тока Ампера сила. Электрический заряд, движущийся в магнитном поле, испытывает действие силы Лоренца. Величина силы Лоренца, действующей на положительный заряд, равна произведению модуля заряда на модуль вектора магнитной индукции и на синус угла между вектором магнитной индукции и вектором скорости заряженного движения:
Направление силы Лоренца определяется по правилу левой руки: если левая рука расположена таким образом, что составляющая магнитной индукции, перпендикулярная скорости заряда, входит в ладонь, а четыре пальца направлены вдоль движения положительного заряд, то большой палец, согнутый под углом 90 °, покажет направление силы Лоренца, действующей на заряд. Для отрицательно заряженной частицы сила Лоренца направлена против направления большого пальца.
Основные понятия и законы электромагнитной индукции
Если через замкнутую проводящую цепь проникает переменный магнитный поток, в этой цепи возникают ЭДС и электрический ток. Эта ЭДС называется ЭДС электромагнитной индукции, а ток – индукцией. Явление их возникновения называется электромагнитной индукцией. ЭДС индукции можно рассчитать по основному закону электромагнитной индукции или по закону Фарадея:
Знак «-» связан с направлением индукционного тока. Это определяется правилом Ленца:
индукционный ток направлен таким образом, что его действие противодействует причине, вызвавшей появление этого тока. Магнитный поток, поступающий в цепь, прямо пропорционален току, протекающему в этой цепи:
Коэффициент пропорциональности L зависит от геометрии цепи и называется индуктивностью или коэффициентом самоиндукции этой цепи. L = 1 ч
Текущую энергию магнитного поля можно рассчитать по формуле
где L – индуктивность проводника, создающего поле; I – ток, протекающий по этому проводнику
Электромагнитные колебания и волны
Колебательный контур – это электрическая цепь, состоящая из последовательно включенных конденсатора с емкостью C и катушки с индуктивностью L (см. Рис.
Для незатухающих свободных колебаний в контуре циклическая частота определяется по формуле
Период свободных колебаний в контуре определяется формулой Томсона:
Если источник переменного напряжения включен в цепь LC последовательно с L, C и R, в цепи возникнут вынужденные электрические колебания. Такие колебания принято называть переменным электрическим током
В цепь переменного тока могут быть включены три типа нагрузок: конденсатор, резистор и индуктор. Конденсатор имеет сопротивление переменному току, которое можно рассчитать по формуле
Ток, протекающий через конденсатор, опережает по фазе напряжение / 2 или четверть периода, а напряжение отстает от тока с таким же фазовым углом. Катушка индуктивности имеет сопротивление переменному току, которое можно рассчитать по формуле
Ток, протекающий через катушку индуктивности, не совпадает по фазе с напряжением на 1/2 или четверть периода. Напряжение опережает ток на тот же фазовый угол.
Трансформатор – это устройство, предназначенное для преобразования переменного тока. Трансформатор состоит из замкнутого стального сердечника, на котором установлены две катушки. Катушка, которая подключается к источнику переменного напряжения, называется первичной обмоткой, а катушка, которая подключается к потребителю, называется вторичной обмоткой. Отношение напряжения на первичной обмотке к вторичной обмотке трансформатора равно отношению количества витков в этих обмотках:
Если K> 1, трансформатор понижающий, если K <1, трансформатор повышающий. Практика: решите 16 задач и вариантов подготовки к экзамену по физике.
Принцип действия
Действие клетки Фарадея основано на том, что заряд, попадая в проводник, распределяется по его поверхности, а внутренняя часть остается нейтральной. Фактически, вся ячейка, состоящая из проводящего материала, представляет собой единственный проводник, «концы» которого приобретают противоположный заряд. Возникающий в результате электрический ток создает поле, которое компенсирует внешнее воздействие. Напряженность электрического поля во внутренней части этой структуры равна нулю.
интересно, что если поле создается внутри ячейки, эффект тоже работает. Однако в этой ситуации заряд будет распределен по внутренней поверхности сетки или другой проводящей плоскости и не сможет проникнуть наружу.
В английской терминологии KF звучит как «щит Фарадея» или «щит / щит Фарадея». Эта концепция хорошо передает суть устройства, которое, как экран или защитный экран, отражает лучи, влияющие на его содержимое.
Способы расчёта
Есть несколько основных способов определения индуктивности катушки. Все формулы, которые будут использоваться при расчетах, легко найти в справочниках или в Интернете. Весь процесс расчета довольно прост и не составит труда для людей с базовыми математическими и физическими знаниями.
Через силу тока
Этот расчет считается самым простым способом определения индуктивности катушки. Формула силы тока исходит из самого термина. Какая индуктивность катушки – можно определить по формуле: L = Ф / I, где:
- L – индуктивность цепи (в генри);
- это величина магнитного потока, измеренная по Веберу;
- I – ток в катушке (в амперах).
Соленоид конечной длины
Соленоид представляет собой длинную и тонкую катушку, у которой толщина намотки намного меньше диаметра. В этом случае расчеты производятся по той же формуле, что и сила тока, только величина магнитного потока будет определяться следующим образом: Ф = µ0NS / l, где:
- µ0 – магнитная проницаемость среды, определяемая по справочным таблицам (для воздуха, которое является значением по умолчанию в большинстве расчетов, оно равно 0,00000126 генри / метр);
- N – количество витков катушки;
- S – площадь поперечного сечения змеевика, измеренная в квадратных метрах;
- l – длина соленоида в метрах.
Коэффициент самоиндукции соленоида также можно рассчитать согласно способу определения энергии магнитного потока поля. Это более простой вариант, но он требует некоторых значений. Формула для определения индуктивности: L = 2W / I 2, где:
- W – энергия магнитного потока, измеренная в джоулях;
- I – ток в амперах.
Катушка с тороидальным сердечником
В большинстве случаев тороидальная катушка наматывается на сердечник из материала с высокой магнитной проницаемостью. В этом случае для расчета индуктивности можно использовать формулу прямого соленоида бесконечной длины. Он имеет следующий вид: L = N µ0 µS / 2 πr, где:
- N – количество витков катушки;
- µ – относительная магнитная проницаемость;
- µ0 – магнитная постоянная;
- S – площадь поперечного сечения сердечника;
- – математическая константа, равная 3,14;
- r – средний радиус тора.
Длинный проводник
Большинство этих квазилинейных проводников имеют круглое поперечное сечение. В этом случае значение коэффициента самоиндукции будет определяться по стандартной формуле для приближенных расчетов: L = µ0l (µelnl / r + µi / 4) / 2 π. Здесь используются следующие условные обозначения:
- l – длина жилы в метрах;
- r – радиус сечения провода, измеряемый в метрах;
- µ0 – магнитная постоянная;
- µi – характеристика относительной магнитной проницаемости материала, из которого сделан проводник;
- µe – относительная магнитная проницаемость внешней среды (чаще всего для вакуума берется значение, равное 1);
- это число пи;
- ln – обозначение логарифма.
Теги: ампер, аппликация, карданный вал, взгляд, повреждение, генератор, двигатель, дом, знак, измерение, как, компьютер, конструкция, цепь, магнит, магнитный, пар, постоянный, потенциал, правило, принцип, провод, работа, размер, поток, самоиндукция, сопротивление, цепь, десять, ток, трансформатор, эффект
Электродвигатель
Электрогенератор может работать в «обратном направлении» и становиться двигателем. Рассмотрим, например, диск Фарадея. Предположим, что через токопроводящее радиальное плечо протекает постоянный ток от определенного напряжения. Таким образом, согласно закону силы Лоренца, на этот движущийся заряд действует сила в магнитном поле B, которая заставляет диск вращаться в направлении, определяемом правилом левой руки. При отсутствии эффектов, вызывающих диссипативные потери, таких как трение или джоулева тепло, диск будет вращаться с такой скоростью, что d ΦB / dt равно напряжению, вызывающему ток.
Закон Фарадея-Максвелла
В 1873 г. Максвелл переформулировал теорию электромагнитного поля. Выведенные из него уравнения легли в основу современной радиотехники и электротехники. Они выражаются следующим образом:
- Edl = -dФ / dt – уравнение электродвижущей силы
- Hdl = -dN / dt – уравнение магнитодвижущей силы.
Где E – напряженность электрического поля в зоне dl; H – напряженность магнитного поля в области dl; N – поток электрической индукции, t – время.
Симметричный характер этих уравнений устанавливает связь между электрическими и магнитными явлениями, магнитными с электрическими явлениями, физический смысл, с которым определяются эти уравнения, может быть выражен следующими положениями:
- если электрическое поле изменяется, то это изменение всегда сопровождается магнитным полем.
- если магнитное поле изменяется, то это изменение всегда сопровождается электрическим полем.
Рис. Возникновение вихревого магнитного поля
Максвелл также обнаружил, что распространение электромагнитного поля равно скорости распространения света.
Что мы узнали?
Ученики восьмых классов должны знать, что явление электромагнитной индукции было впервые обнаружено Майклом Фарадеем. Он доказал, что электрическое и магнитное поля имеют общую природу. Независимые исследования, основанные на экспериментах Фарадея, также были проведены такими великими фигурами, как Ленц и Максвелл, которые расширили наши знания об электромагнитном поле.
Явление электромагнитной индукции
Электромагнитная индукция – явление возникновения тока в замкнутой проводящей цепи при изменении пронизывающего ее магнитного потока.
Явление электромагнитной индукции было открыто М. Фарадеем.
- Две катушки были намотаны на токонепроводящей основе: витки первой катушки располагались между витками второй. Витки одной катушки были замкнуты на гальванометр, а другая была подключена к источнику тока. Когда ключ был закрыт и ток прошел через вторую катушку, в первой появился импульс тока. Когда ключ был открыт, также наблюдался импульс тока, но ток через гальванометр протекал в обратном направлении.
- Первая катушка была подключена к источнику тока, вторая, подключенная к гальванометру, перемещалась относительно него. При приближении или удалении катушки регистрировался ток.
- Катушка закрыта для гальванометра, и магнит движется – входит (выходит) – относительно катушки.
Эксперименты показали, что индукционный ток возникает только при изменении линий магнитной индукции. Направление тока будет разным при увеличении количества линий и при их уменьшении.
Сила индукционного тока зависит от скорости изменения магнитного потока. Само поле может меняться или граница может двигаться в неоднородном магнитном поле.
Пояснения к возникновению индукционного тока
Ток в цепи может существовать, когда на свободные заряды действуют внешние силы. Работа этих сил по перемещению одиночного положительного заряда по замкнутой цепи равна ЭДС. Это означает, что при изменении количества магнитных линий на граничной поверхности в ней появляется ЭДС, которая называется ЭДС индукции.
Электроны в неподвижном проводнике могут быть приведены в движение только электрическим полем. Это электрическое поле создается изменяющимся во времени магнитным полем. Это называется вихревым электрическим полем. Понятие вихревого электрического поля было введено в физику великим английским физиком Дж. Максвеллом в 1861 году.
Свойства паразитного электрического поля:
- источник – переменное магнитное поле;
- обнаруживается по действию на заряд;
- это не потенциал;
- силовые линии замкнуты.
Работа этого поля при движении одиночного положительного заряда по замкнутому контуру равна ЭДС индукции в неподвижном проводнике.
Самоиндукция
Самоиндукция – это явление индукции ЭДС в проводнике в результате изменения тока в нем.
Когда ток в катушке изменяется, магнитный поток, создаваемый этим током, изменяется. Изменение магнитного потока, поступающего в катушку, должно вызывать появление в катушке ЭДС индукции.
В соответствии с правилом Ленца, ЭДС самоиндукции предотвращает увеличение тока при включении цепи и уменьшает ток при выключении цепи.
Это приводит к тому, что при замкнутой цепи, в которой присутствует источник тока с постоянной ЭДС, через некоторое время устанавливается сила тока.
При отключении источника питание также не прекращается мгновенно. Результирующая ЭДС самоиндукции может превышать ЭДС источника.
Явление самоиндукции можно наблюдать, собрав электрическую цепь из катушки с высокой индуктивностью, резистора, двух идентичных ламп накаливания и источника тока. Резистор должен иметь такое же электрическое сопротивление, что и провод катушки.
Опыт показывает, что при замкнутой цепи электрическая лампа, соединенная последовательно с катушкой, загорается немного позже, чем лампа, соединенная последовательно с резистором. Росту тока в цепи катушки при включении препятствует ЭДС самоиндукции, возникающая при увеличении магнитного потока в катушке.
При отключении питания оба индикатора мигают. В этом случае ток в цепи поддерживается ЭДС самоиндукции, возникающей при уменьшении магнитного потока в катушке.
ЭДС самоиндукции прямо пропорциональна индуктивности катушки и скорости изменения тока в катушке.
Индуктивность
Следовательно, магнитный поток через цепь прямо пропорционален току в цепи:
Индуктивность – это коэффициент пропорциональности (L ) между током (I ) в цепи и магнитным потоком ( Phi ), создаваемым этим током:
Индуктивность зависит от размера и формы проводника, от магнитных свойств среды, в которой находится проводник.
Единица измерения индуктивности в системе СИ – Генри (Гн). Индуктивность контура равна 1 генри, если при постоянном токе 1 ампер магнитный поток через контур равен 1 Веберу:
Можно дать второе определение единицы индуктивности: элемент электрической цепи имеет индуктивность 1 Гн, если при равномерном изменении тока в цепи 1 ампер за 1 с ЭДС самоиндукции составляет В нем появляется 1 вольт.
Энергия магнитного поля
Когда индуктор отключен от источника тока, лампа накаливания, подключенная параллельно катушке, излучает короткую вспышку. Ток в цепи возникает под действием ЭДС самоиндукции.
Источником энергии, выделяющейся при этом в электрическую цепь, является магнитное поле катушки.